Dvärgnovan UZ Boo i sällsynt utbrott
Hem › Observationer › Variabla stjärnor › Dvärgnovan UZ Boo i sällsynt utbrott
- Detta ämne har 96 svar, 5 deltagare, och uppdaterades senast 24-09-12 19:57 av
Hans Bengtsson.
-
FörfattareInlägg
-
-
8 augusti, 2024 kl. 16:48 #9125
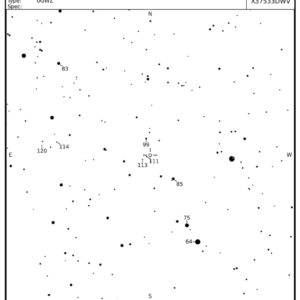
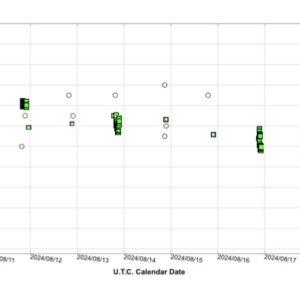
Dvärgnovan UZ Boo rapporteras vara i utbrott, en sällsynt händelse!
https://www.aavso.org/vsx/index.php?view=detail.top&oid=4342
En Astronet-tråd angående utbrottet år 2013:
http://astronet.se/phpBB3/viewtopic.php?t=7743
Det utbrott som nu har påbörjats upptäcktes för en kort stund sedan från Japan. Fotometri och andra obsar redan i natt (8-9 augusti) är förstås av stort värde. Kanske MWT?
Uppdatering:
ASAS-SN har fångat utbrottet, se klipp nedan.
Edit:
Upptäckten av UZ Boo (HV 10426) skedde ganska tidigt, vid genomgång av Harvard-plåtar, och publicerades 1940 (se klipp). De utbrott som upptäckarna Hanley och Shapley hittade ägde rum 12 april 1890, 1 april 1929, 5 juni 1937 och 30 maj 1938. Man får säga att tidsintervallet mellan de två sistnämnda utbrotten var förvånansvärt litet.
Jag tror att denna lista över kända utbrott är komplett:
1890 april
1929 april
1937 juni
1938 maj
1978 september
1994 augusti
2003 december
2013 juli
2024 augusti
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
-
Detta ämne redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Detta ämne redigerades för 1 år av
-
8 augusti, 2024 kl. 23:45 #9135
-
9 augusti, 2024 kl. 08:19 #9143
Körde en V-serie med MWT i natt 8 Aug 21:00-23:00 UT men tycker inte man kan utläsa några tydliga superpucklar. Den förväntade perioden borde vara kring 0,062d, alltså 1,5h om jag uppfattat det rätt? En hel period borde i så fall kunnat rymmas i tidsserien.
Kan det vara så att de framträder tydligare i ett senare skede?
Edit: Tog även ett par bilder i BRI och det är inga stora skillnader mellan banden. R är ljusare än I, men det kan bero på det större felet hos I-jämförelsestjärnorna.
/David
SVO: DHE
AAVSO: HDAE-
Det här svaret redigerades för 1 år av
davhei.
Attachments:
-
Det här svaret redigerades för 1 år av
-
9 augusti, 2024 kl. 09:34 #9146
Häftigt!
Det är tydligt att tidsserien är gjord något före den exakta magnitudtoppen, ljusstyrkan ökar en aning under seriens gång. Jag tror att superpucklarna ännu inte hunnit utvecklas, men att de snart dyker upp.
Man kan säga att ett välbekant mönster upprepades: ett intressant utbrott upptäcks i Japan, vi rapporterar några timmar senare på SAAF:s forum, och innan mörkret hunnit till USA så gör SAAF-observatörerna sina obsar. Eftersom japanerna inte brukar skicka till AAVSO utan till sin egen variabelorganisation, så blir SAAF allt emellanåt allra först i AAVSO…
En länk till UZ Boo och många andra dvärgnovor ges nedan, liksom ett klipp från den artikeln.
https://arxiv.org/pdf/0905.1757
Det är förresten svårt att tänka sig något bättre sätt att använda MWT än just detta. Jag har aldrig träffat någon person som varit lika entusiastisk över sällsynta utbrott som Margareta Westlund.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
10 augusti, 2024 kl. 12:40 #9169
Hej!
Nattens tidsserie:
Inga tydliga superpucklar. Det är en del underliga outliers här (lägre magnituder) som jag är igång med att försöka analysera. I stort sett ser magnituderna på ref-, check, och jämförelsestjärnor jämna ut och hög SNR, så lite lätt mystiskt. Jag tenderar i alla fall att se bort from dem än så länge.
Edit: efter att ha noggrannt analyserat om serien några gånger försvinner de mesta av de där underliga mätningarna och mycket små variationer blir kvar, troligen mest brus.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294-
Det här svaret redigerades för 1 år av
 Magnus Larsson.
Magnus Larsson.
-
Det här svaret redigerades för 1 år av
-
11 augusti, 2024 kl. 08:21 #9172
Körde en tidsserie med MWT även i natt. Några BRI och en serie i V. Bifogat är V-mätningar daterade 10 augusti 21:10 – 22:50 UT.
Sedan den tidigare serien jag tog för två dagar sedan har dvärgnovan blivit ungefär 0,15 magnituder ljussvagare. R och I har närmat sig varandra.
Tycker mig inte se någon tydlig tendens till superpucklar, möjligen går det med god vilja och önsketänkande att ana en period kring 0,06 och en amplitud om ungefär 0,015 magnituder, men det är inget jag skulle våga dra några stora växlar på.
Vad tror ni?
/David
SVO: DHE
AAVSO: HDAEAttachments:
-
11 augusti, 2024 kl. 11:51 #9175
Helt lysande resultat!
Magnus:
Din tidsserie från natten 9-10 augusti finns inte i SVO, meddelas från leg. SVO-kontrollanten (dvs undertecknad). Kommer nog snart, vi väntar otåligt …
David:
Du råkade skriva att UZ Boo avtagit med 1.5 mag, ska nog vara 0.15 mag.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
-
11 augusti, 2024 kl. 12:15 #9178
Helt rätt Hans, tack! Jag editerar.
/David
/David
SVO: DHE
AAVSO: HDAE -
11 augusti, 2024 kl. 12:40 #9180
Hej!
Nu är de där. Phoranso strulade för mig och producerade rapporter som inte gick att ladda upp. Väldigr bra program – när det funkar….;)
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
12 augusti, 2024 kl. 11:36 #9184
UZ Boo ligger bra till från min balkong, och himlen såg rätt lovande ut i skymningen. Tyvärr kom det in cirrus åt det hållet när jag försökte, gränsmagnituden blev usel med 8-tummaren. Jag kunde med viss möda men utan tveksamhet se 121-stjärnan. Under ett kort ögonblick tyckte jag att jag nog skymtade även UZ Boo, i så fall av mag ca 13, men det var så osäkert att det fick bli en negativ skattning.
Himlen hade en rödaktig färg som troligen var rött norrsken, och det underlättade inte, men i första hand var det envisa cirrus som sabbade möjligheten att göra en positiv obs av UZ Boo. Får se om det blir bättre ikväll.
T CrB gick förstås smidigt att obsa. Råkade också se en perseid av mag 2 nära horisonten rakt västerut.
-
12 augusti, 2024 kl. 16:15 #9194
Hej!
Nattens skörd:
Denna gång V-filter. Inte mkt till pucklar där inte…..
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
12 augusti, 2024 kl. 16:42 #9195
Så himla bra!
Att den var så ljusstark innebär förmodligen också att jag verkligen såg den när jag tyckte jag gjorde det … jag antecknade först positiv obs 12.8 men ändrade mig till negativ 12.1 innan jag rapporterade. Detta efter att ha ställt mig själv frågan om jag kunde ta gift på att jag sett den, och jag svarade nej på det. Befinner mig ibland i gränslandet mellan försiktig general och fegis … 😀
-
13 augusti, 2024 kl. 17:16 #9226
Hej!
Kanske, kanske antydan till lite svängningar….?
Jag laddade av misstag upp en fil på SVO med för mkt brus-obsar där mot slutet, men så här ser den rensade versionen ut (har försökt städa ut de som blev fel….).
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
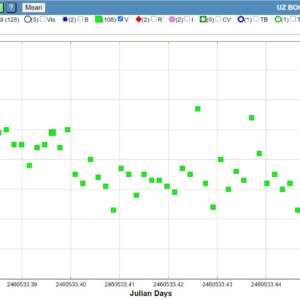
13 augusti, 2024 kl. 17:30 #9233
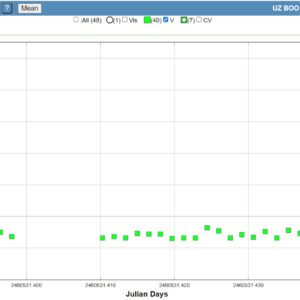
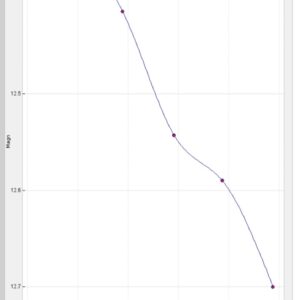
Enormt många mätningar av UZ Boo på bara några få dygn! Kanske kan superpucklar börja visa sig nu?
Dygnsmedelvärden av V-mätningarna visas i kurvan nedan.
Attachments:
-
14 augusti, 2024 kl. 17:37 #9253
Hej!
Det blir många mätningar när den är så stark, jag kör på 30 sek så här länge, får nog köra längre framöver dock. Och nu kommer nog några kvällar med moln.
Här är gårkvällens skörd. Nog verkar det vara lite svängning även om den är liten:
Taget med en C11 med en QHY268m, V-filter, i min trädgård i Malmö.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
17 augusti, 2024 kl. 00:54 #9261
Här kommer en färsk V-serie på en dryg timme från MWT i Oria, ikväll den 16:e aug:
/David
SVO: DHE
AAVSO: HDAE-
Det här svaret redigerades för 1 år av
davhei.
Attachments:
-
Det här svaret redigerades för 1 år av
-
17 augusti, 2024 kl. 09:20 #9266
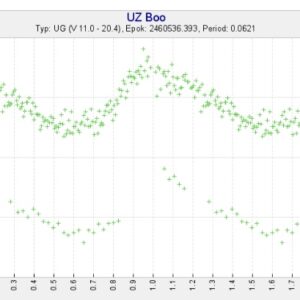
Fantastiskt bra gjort!
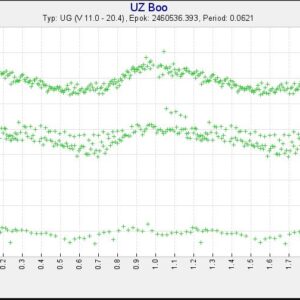
Ingen tvekan alls om att ni fångat superpucklar. Jag testade med att i SVO lägga in V-obsarna från kvällen 13 aug (den ljusare serien) och kvällen 16 aug. Blev utmärkt resultat med de element för max som jag använde.
Attachments:
-
17 augusti, 2024 kl. 09:45 #9269
Snyggt analyserat Hans!
Jag hade gärna kört en längre serie men var begränsad av tiden då teleskopet aktiveras för kvällen och när objektet sjunkit för lågt.
/David
SVO: DHE
AAVSO: HDAE -
17 augusti, 2024 kl. 12:30 #9270
Den berömde ukrainske professorn i astronomi Ivan L Andronov, specialist på variabla stjärnor, gratulerar på Facebook.
Attachments:
-
17 augusti, 2024 kl. 13:01 #9272
-
17 augusti, 2024 kl. 19:27 #9280
ToM bör betyda ”time of maximum”, precis som du skriver.
-
18 augusti, 2024 kl. 08:26 #9281
Apropå UZ Boo. Eftersom det verkar finnas ett samband mellan superpucklarnas period och det binära systemets omloppstid, jag tolkar det som att de skiljer sig åt endast med några procent kopplade till ackretionsskivans precession, så undrade jag om jag grovt kunde räkna ut komponenternas separation.
Jag lekte med en formel jag hittade, baserad på Keplers tredje lag:
a^3 = G(M1+M2)P^2 / 4π^2
där
a = Genomsnittliga separationen mellan komponenterna i meter
G = Gravitationskonstanten 6,6743×10^-11 m^3 kg^-1 s^-2
M1 & M2 = Kropparnas massor i kg
P = Omloppstiden i sekunderoch man får då om man antar massor för båda kropparna motsvarande en solmassa vardera och en omloppstid enligt den uppmätta perioden om 1,5h en separation på ungefär 600 000 km.
Avståndet ändras inte särskilt mycket om massorna halveras eller dubblas.
Det ger kanske en fingervisning om skalorna. En solradie mellan dem ungefär, möjligen i kontakt med varandra.
Kollade mina siffror mot en kalkylator jag hittade så jag inte snurrade bort mig fullständigt men den ger liknande resultat:
https://www.omnicalculator.com/physics/kepler-third-law
/David
SVO: DHE
AAVSO: HDAE-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
-
18 augusti, 2024 kl. 12:35 #9288
Hej!
Och här är en serie i V-bandet från igårkväll:
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
18 augusti, 2024 kl. 14:43 #9289
-
18 augusti, 2024 kl. 15:28 #9291
Hans,
Är det Peranso du använder för fasdiagrammen eller finns funktionen någonstans i SVO?
/David
SVO: DHE
AAVSO: HDAE-
18 augusti, 2024 kl. 15:44 #9292
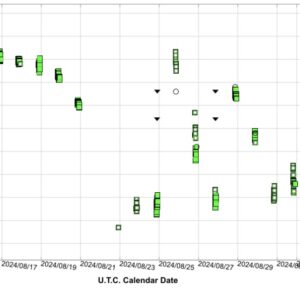
Funktionen finns i SVO. Man väljer Rita ljuskurva, visa fas (1 eller 2), skriver in maxdatum och period – här har jag använt de element som Hans använder – och så kan man indikera hur många dygn bakåt man vill se alternativt start/slutdatum.
Här är de senaste två dygnen:
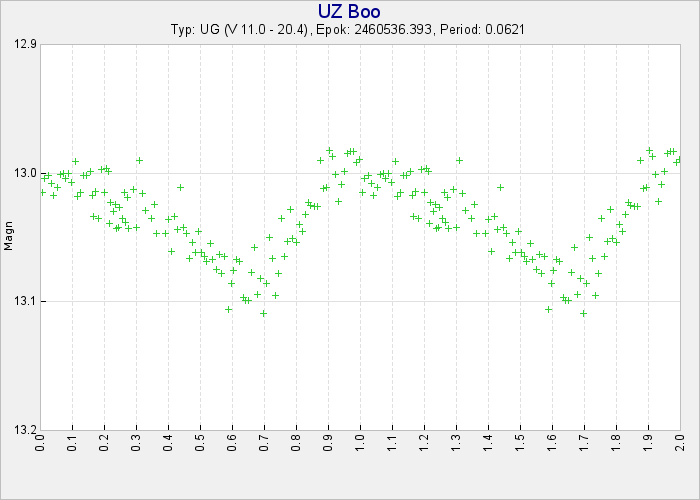
-
Det här svaret redigerades för 1 år av
Gustav Holmberg.
Attachments:
-
Det här svaret redigerades för 1 år av
-
-
18 augusti, 2024 kl. 15:49 #9295
David:
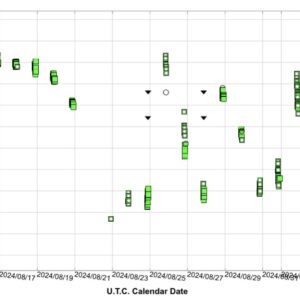
Jag använder bara SVO, se klipp nedan. Peranso skulle förstås bli mera exakt men jag tycker SVO duger bra som en snabbvariant (har inte Peranso).
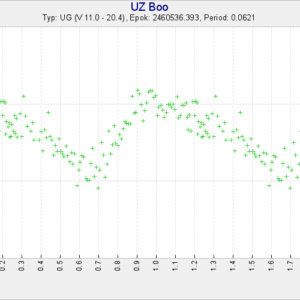
Började med att testa med perioden som finns publicerad, och justerade sedan decimalerna så att dina och Magnus serier gav samma kurva. Därefter justerade jag utgångsmaximet så att fasen där blev 1.0. Allt bara med ögonmått …
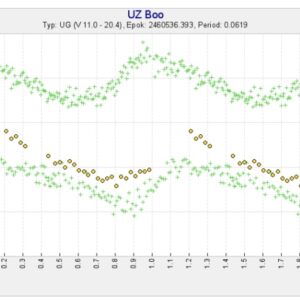
PS:
Som ett exempel som visar hur noggrann SVO-metoden faktiskt är, så kan vi ändra perioden 0.0621 dygn en liten aning till 0.0619 dygn, vilket är (ungefär) den publicerade perioden. Omedelbart ser vi då att de två senaste serierna inträffar rejält mycket för sent, alltså är 0.0619 dygn en alltför kort period, medan 0.0621 blir bra. Se klipp nedan med 0.0619 dygn.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
18 augusti, 2024 kl. 16:23 #9299
Tack Gustav och Hans. Jag ska leka lite med funktionen.
/David
SVO: DHE
AAVSO: HDAE -
18 augusti, 2024 kl. 17:12 #9300
Hej!
Jag försöker med Peranso men jag är inte tillräckligt bra på den här sortens analyser när det är så stora glapp mellan obsarna som flera dar (jag fixar det om det är en sammanhängande serie :)). Intressant nog är det i stort sett bara våra svenska obsar som finns på AAVSO också, så det hjälpte inte att försöka ladda ner därifrån. Men jag lyckas inte replikera den där perioden på ca 0,0619 dagar. Dvs: jag får fram en topp ungefär där, men också flera andra toppar runt omkring som verkar ungefär lika starka… kanske Thomas kan bistå med lite Peranso-magi…? 🙂
Vad gäller din beräkning av avstånd, David, hittar jag heller ingen info om det från andra källor – har ni andra hittat det? Vore intressant om man kunde mäta P-orb ju, på nåt vettigt sätt också 🙂 Men ja, det är inte så lätt när det inte är förmörkelser.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
18 augusti, 2024 kl. 18:07 #9301
Jag testade med Peranso, men fick inte heller någon entydig period från Magnus och Davids obsar i SVO. Jag fick ungefär likvärdiga periodalternativ för 0.0504, 0.0531, 0.0561, 0.0594 och 0.0632, utöver dessa finns en massa andra periodkandidater. Det finns en liten topp för 0.0621, men det fanns ett 20-tal andra alternativ som får högre utslag. För att kunna avgöra behövs nog en eller ett par hela cykler under samma natt.
Superpuckelperioden är väl inte heller konstant. Det brukar talas om olika faser under ett utbrott, A-stage, B-stage osv. där perioden är lite annorlunda. eller ändrar sig på olika sätt. Har det inte i huvudet just nu och vet inte heller hur det spelar in på UZ Boo.
-
18 augusti, 2024 kl. 19:19 #9302
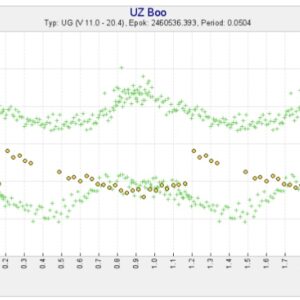
Jag testade i SVO med de fem kandidatperioderna du nämner, på de tre senaste serierna (när superpucklar hunnit utvecklas) men ingen av dessa ger ”träff” på Davids serie. Däremot passar 0.0621 dygn bra för alla tre serierna. Så jag tänker att Peranso kanske har överprioriterat Magnus två serier genom att dessa innehåller fler mätningar?
Exempelvis ger den första perioden du nämner, 0.0504 dygn, resultatet i klippet nedan.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
18 augusti, 2024 kl. 19:50 #9306
Det kan nog vara så Hans, att serierna med fler obsar viktar resultaten i fel riktning. Jag kollade inte så noga manuellt vilka lösningar som visuellt ser bäst ut. I fall som detta är kan nog den manuella granskningen vara lika viktig som vad periodalgoritmerna får fram.
-
Det här svaret redigerades för 1 år av
-
18 augusti, 2024 kl. 21:00 #9307
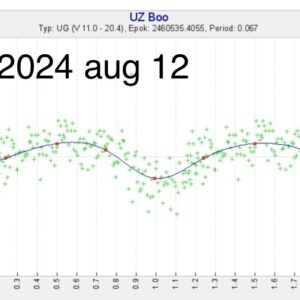
Det finns faktiskt superpucklar om man isolerar serien från 12 augusti, men med mycket liten amplitud, det var inte förrän dygnet efter de blev påtagliga.
När jag satte in perioden 0.067 dygn och perioder däromkring fick jag ett skapligt utslag för 12 augusti, men det är ju svårt att veta exakt från en enskild serie med så liten amplitud. Perioden 0.0621 dygn tycks inte funka när man jämför 12 aug med efterföljande serier.
Attachments:
-
18 augusti, 2024 kl. 21:38 #9309
Hej!
Spännande! Gary Poyner i brittiska VSS ber oss fortsätta också 😉 Jag är lite aktiv där med.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
18 augusti, 2024 kl. 22:15 #9310
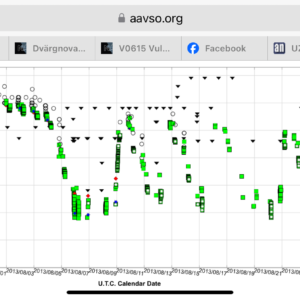
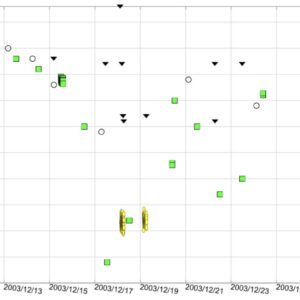
Vid utbrottet 2013 återljusnade UZ Boo fyra gånger, se diagram. Man kan undra om något liknande kommer att ske nu.
Edit:
Jag ser nu att stjärnan återljusnade fyra gånger även i samband med utbrottet 2003!
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
19 augusti, 2024 kl. 10:04 #9312
Ska försöka få till ett par tidsserier i veckan med MWT. Återkommer.
/David
SVO: DHE
AAVSO: HDAE -
19 augusti, 2024 kl. 10:55 #9317
David:
Det låter väldigt bra!
Ganska sannolikt är att UZ Boo under de närmaste dygnen kommer att tvärdyka i ljusstyrka till magnitud 17, för att därefter under några veckor vid flera tillfällen återljusna till mag 13-14. Detta baserat på hur stjärnan uppförde sig både 2003 och 2013. Men det kan förstås bli annorlunda den här gången.
Man kan undra om det finns superpucklar under de korta sekundära topparna (återljusnanden). Nog ingen som vet? Det vore förstås enastående bra med tidsserier under eventuella sådana toppar.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
-
19 augusti, 2024 kl. 11:04 #9318
Jag har nu gjort en lite noggrannare analys i Peranso av UZ Boo. Den här gången använde jag AAVSO-data där det förutom våra obsar fanns två kortare serier från Ian Sharp. Nu tyckte även Peranso att bästa perioden är 0.06211.
I artikeln https://arxiv.org/pdf/0905.1757 av Taichi Kato finns två superpuckelperioder angivna: 0.061743 från utbrottet 1994 och 0.061922 från utbrottet 2003. Alltså lite kortare än den vi fått fram.
-
19 augusti, 2024 kl. 11:48 #9322
Thomas:
Känns tryggt att Peranso och SVO nu är överens!
Vet du om DASCH täcker detta område?
-
19 augusti, 2024 kl. 12:20 #9324
Den finns med i DASH. Jag hittade positiva obsar med dessa datum: 1929-03-18, 1929-03-20, 1934-05-17, 1938-06-01, 1938-06-02 och 1938-06-03. Utbrotten 1929 och 1938 var med i din lista. Ev. kan den ha haft ett utbrott även 1934.
-
19 augusti, 2024 kl. 13:17 #9325
Hej!
Vad är DASH? Kan inte vara detta ni menar:
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
19 augusti, 2024 kl. 13:17 #9326
Det är ju bingo om du hittat ett tidigare okänt utbrott 1934! Vore spännande att se den bilden här i tråden. Borde meddelas till AAVSO om det känns säkert, annars finns risken att nån annan hinner före med att kolla DASCH.
De två andra utbrotten du hittade är ju på bilder tagna vid något annorlunda datum än de datum som publicerats (se klipp jag tidigare gett). Betyder att utbrotten mera exakt kan dateras. Förresten lite överraskande att de bilder du hittade missades när de fyra gamla utbrotten publicerades. Förmodligen hade de inte tillgång till exakt de bilder som finns i DASCH.
-
19 augusti, 2024 kl. 13:20 #9327
DASCH:
https://en.m.wikipedia.org/wiki/Digital_Access_to_a_Sky_Century_@_Harvard
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
-
19 augusti, 2024 kl. 14:21 #9329
Här är 3 bilder från DASCH. När jag tittar närmare och mäter avståndet mellan stjärnorna verkar utbrottet 1934 skumt. Det verkar snarare vara en grannstjärna än UZ Boo på den bilden. Grannstjärnan syns svagt på de andra bilderna också. Antagligen har stjärnorna som ligger nära varann blivit felidentifierade i DASCH på 1934-bilden.
Attachments:
-
19 augusti, 2024 kl. 15:05 #9333
Aha, det var ju lite synd! DASCH identifierar ibland fel, om man ger positionen händer det att programmet helt enkelt tar ID från närmaste stjärnan även om positionen inte helt stämmer. Jag råkade ut för detta en gång när jag trodde jag hittat ett gammalt utbrott (har glömt vilken stjärna), men upptäckte då att det var en grannstjärna. Och en gång var det en sekundärbild av en stjärna som uppstått av att två exponeringar hade slagits samman till en bild utan perfekt anpassning.
Så DASCH är lite lurigt men förstås en fantastisk resurs.
Man kan också fundera på om utbrottet 5 juni 1937, som upptäckarna rapporterade, verkligen existerade. Magnituden ges som 13.7: dvs ungefär 13.7. Kanske tveksam ID? Intervallet mellan utbrotten 1937 och 1938 är verkligen överraskande litet.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
-
20 augusti, 2024 kl. 10:51 #9337
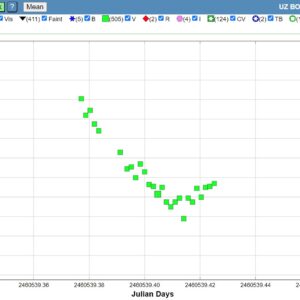
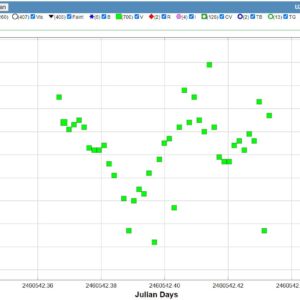
En V-serie från MWT i Oria inatt på ungefär 1,5h. Här har det blivit betydligt svårare att urskilja variationer jämfört med obsarna för ett par dagar sedan. Möjligen anar man att det fortfarande finns pucklar i fasdiagrammet där serierna från den 13:e, 16:e och 17:e lagts in tillsammans med nattens.
Dippen kring 2460542.42 är jag mycket tveksam till om den är verklig. Det fanns avvikare hos båda jämförelsestjärnorna men som drog åt olika håll.
Det var fullmåne inatt vilket knappast förbättrat mätningarnas kvalitet.
/David
SVO: DHE
AAVSO: HDAE-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
-
Det här svaret redigerades för 1 år av
davhei.
Attachments:
-
Det här svaret redigerades för 1 år av
-
20 augusti, 2024 kl. 12:11 #9344
Hej!
En serie från Malmö:
Svårt att se pucklar där….
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
20 augusti, 2024 kl. 14:50 #9347
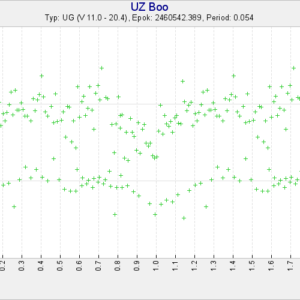
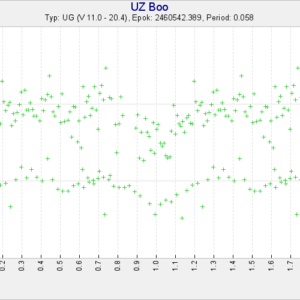
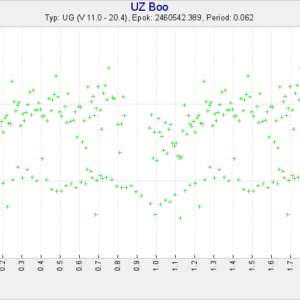
Lade in mina och Magnus obsar från gångna natten i ett diagram där jag valt startpunkt vid ett minimum 2460542,389 och jag vet inte om jag drabbas av önsketänkande, men jag tycker mig se en överensstämmelse vid en period i närheten av 0,058. Blinkar man de bifogade bilderna och jämför med perioder om 0,062 och 0,054 kan man tänka sig att den gemensamma perioden är någonstans mellan dem.
Eller så letar jag mönster där inget finns.
/David
SVO: DHE
AAVSO: HDAE -
20 augusti, 2024 kl. 15:49 #9351
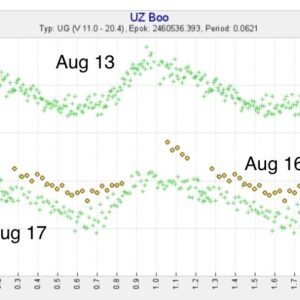
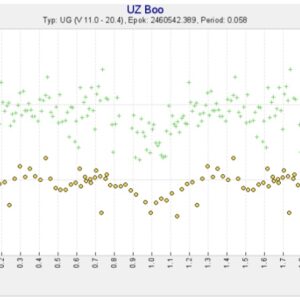
Det verkar som om superpucklarna finns kvar men nu är på väg att försvinna.
På båda serierna ser man ett ganska tydligt minimum vid en och samma tidpunkt. Sedan verkar maximet vara flackt med en tendens till sekundärminimum (?) en halv period in i cykeln.
Jag lånade ett av Davids diagram och ändrade genom att markera hans obsar med gul färg (den möjligheten finns i SVO), för att tydligare visa vilka obsar som hör till vilken serie.
Attachments:
-
20 augusti, 2024 kl. 16:18 #9353
Hej!
Ja det känns bra att ha kunnat bidra med nåt som mest ser ut som en kaotisk bisvärm… 🙂
Det här med att superpucklarna blir mindre tydliga, det överraskar mig. Att de ändrar karaktär, A-, B- och C-typ, det känner jag till – men att de skulle tona bort innan stjärnan falnat mer….?
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
21 augusti, 2024 kl. 10:49 #9356
Den förväntade störtdykningen ner mot magnitud 17 har nog inletts nu, se AAVSO-diagram. Därefter kommer stjärnan förmodligen att återljusna några gånger innan det är dags för slutavtagandet mot magnitud 20.
UZ Boo är verkligen en hyperintressant dvärgnova!
Attachments:
-
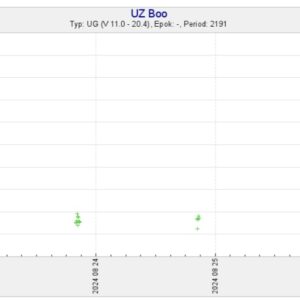
24 augusti, 2024 kl. 14:03 #9379
-
24 augusti, 2024 kl. 14:40 #9380
Det var ju för himla väl att dyket kom nu. Annars hade jag fått köpa mörka solglasögon för att våga visa mig ute bland folk.😀
Återstår bara några snabba stigningar till mag 13 eller 14 så är lyckan total.
Attachments:
-
26 augusti, 2024 kl. 08:20 #9389
Hej!
Here we go… riktig berg-och-dal-bana:
Den har alltså stigit ca 3 magnituder på ett dygn och är nu på väg ner igen… Jag hann inte anpassa min exponeringsserie så det här Clear-filter, 5 min. Få se hur det ser ut ikväll.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
26 augusti, 2024 kl. 09:47 #9390
Fint fångat Magnus!
Oria har haft svårberäkneliga moln ett antal kvällar så jag har avbrutit flera planerade pass. Förhoppningsvis kommer möjligheter senare i veckan.
/David
SVO: DHE
AAVSO: HDAE -
26 augusti, 2024 kl. 12:15 #9391
Ber att få gratulera!
Det hör ju inte precis till vanligheterna att fånga ett ”efterskalv” hos UZ Boo, i all synnerhet som huvudutbrotten kommer en gång per decennium eller något sådant.
Attachments:
-
27 augusti, 2024 kl. 11:22 #9402
Kvällen den 26 augusti hade UZ Boo avtagit till V-magnitud ca 15, enligt mätningar i disigt väder av Ian Sharp, UK.
-
27 augusti, 2024 kl. 17:10 #9408
Hej!
Ca 14.6 här igårkväll.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
27 augusti, 2024 kl. 19:04 #9410
Om man tittar på obsarna från kvällarna 25 och 26 augusti kan man faktiskt få intrycket att det handlar om avtaganden från två separata ”efterskalv”. Kan det ha smugit sig in en topp på dagen den 26 augusti?
Edit: Nej med nya obsar tillgängliga verkar det inte troligt med en extra topp mitt på dagen den 26 augusti.
Diagram från AAVSO, se nedan.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
27 augusti, 2024 kl. 22:02 #9413
Hej!
Spännande. Tyvärr hinns ju bara några få obsar innan den står för lågt – annars kunde man följt rörelserna mer….
Ca 16, C-filter, ikväll.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
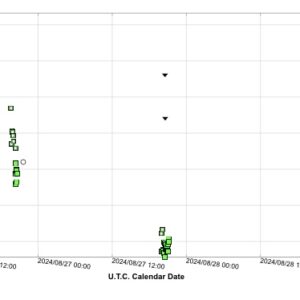
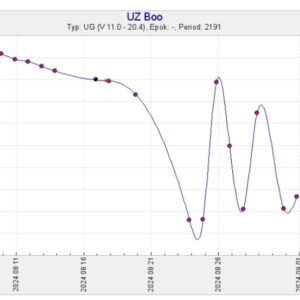
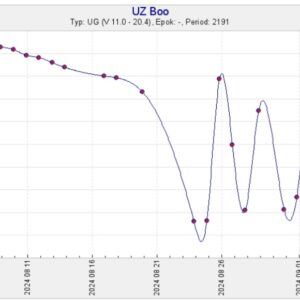
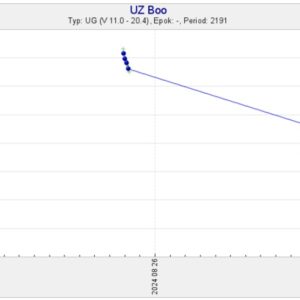
28 augusti, 2024 kl. 13:28 #9417
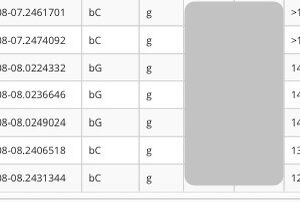
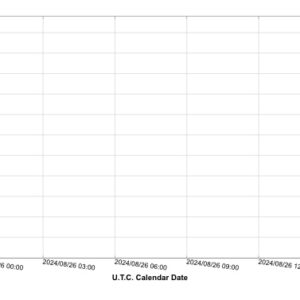
ASASSN-data visar att UZ Boo var osynlig aug 08.24 UT, vilket bör betyda svagare än g 16 eller g 17 (ingen gränsmagnitud anges för dessa obsar). Redan aug 09.00 UT var g 12.2.
Det kan noteras att upptäckten vid magnitud 12.9 skedde aug 08.53 UTC, dvs endast 7 timmar efter den negativa ASASSN-obsen. Stjärnan måste ha ljusnat med minst 3 magnituder under denna korta tid!
Kurvan följer sedan vad vi redan vet från SVO. Mest intressant:
Aug 23.0 UT: g 17.0
Aug 26.0 UT: g 13.9
Aug 28.1 UT: osynlig, svagare än g 15.9.
Aktuell SVO-kurva bifogas också.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
28 augusti, 2024 kl. 22:13 #9432
-
28 augusti, 2024 kl. 22:39 #9433
Magnus,
Jag kör en V-serie med MWT just nu och håller med dig!
/David
SVO: DHE
AAVSO: HDAE -
28 augusti, 2024 kl. 22:40 #9434
Stiligt! 🙂 Jag kan inte fortsätta många minuter till, kanon om du kan (MWT ligger ju lite väster om Malmö…..). Mina drygt 10 bilder visar en ganska jämn kurva så här långt, inget tydligt avtagande.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
28 augusti, 2024 kl. 23:06 #9435
Häftigt!
Jag har via Facebook meddelat Ian Sharp i England, vet inte hur vädret är där, om det är bra så kan han kanske hålla på lite längre pga att han bor ett stycke väster om oss.
-
28 augusti, 2024 kl. 23:15 #9436
Hej!
Kanon! Kan du posta på vsnet också? Eller pinga nån i USA? Så kanske vi kan följa hela puckeln…
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
28 augusti, 2024 kl. 23:39 #9437
Jag postade på fb-gruppen ”Cataclysmic Variables”. Tyvärr är den gruppen måttligt aktiv så jag vet inte om det ger något resultat.
-
28 augusti, 2024 kl. 23:53 #9438
Ingen tydlig tendens till förändring under den timme jag kunde köra en V-serie med MWT. Håller sig kring V-mag 13,8
/David
SVO: DHE
AAVSO: HDAE -
29 augusti, 2024 kl. 09:27 #9439
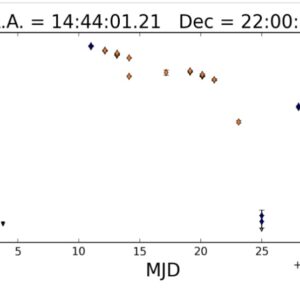
Det håller på att bli en rätt unik obs-serie av UZ Boo, trots att det (åtminstone inom AAVSO, kanske görs något i Japan?) mest är SAAF och Ian Sharp som håller på.
Sharp bidrog med en serie den gångna kvällen (28 aug) som bekräftar SAAF:s obsar.
Edit:
Från Mario Morales Aimar (Mallorca) har nu också inkommit en V-serie för UZ Boo kvällen 28 aug.
Jag har nu i fb-gruppen ”Cataclysmic Variables” särskilt påpekat att det vore bra med obsar även från andra longituder än Europa.
Diagram: AAVSO.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
29 augusti, 2024 kl. 09:43 #9441
Hej!
Tyvärr ser det ut att bli molnigt här ikväll – David, har du tid på MWT?
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
29 augusti, 2024 kl. 10:08 #9445
Magnus,
Nej tyvärr, det verkar bli moln även i Spanien ikväll.
/David
SVO: DHE
AAVSO: HDAE -
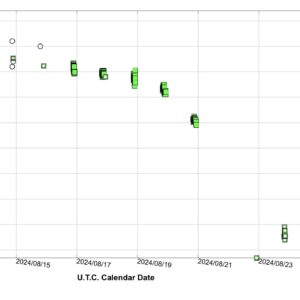
30 augusti, 2024 kl. 11:32 #9450
Värdefulla V-data kunde tas av Ian Sharp igår kväll (29 augusti). Mycket bra samarbete!
Attachments:
-
31 augusti, 2024 kl. 09:03 #9457
Hej!
Ca mag 16 med C-filter igårkväll:
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
31 augusti, 2024 kl. 11:56 #9458
Det är ju lysande!
Krävs nästan obsar varje kväll om man ska få ett bra grepp om händelseutvecklingen nu under transitionsstadiet med efterskalven.
Med lite matjord i fickorna är det inte omöjligt att få en obsserie mitt under det supersnabba stiget till en eftertopp. Men då behövs tur eftersom tidsfönstret på kvällen är så begränsat.
Nu i natt (31 aug – 1 sep) kan det möjligen vara dags för tredje efterskalvet?
-
1 september, 2024 kl. 13:46 #9467
Hej!
Inget efterskalv igår – jag hade den på ca 15.6 med C-filter. Kanske idag?
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294-
Det här svaret redigerades för 1 år av
 Magnus Larsson.
Magnus Larsson.
-
Det här svaret redigerades för 1 år av
-
1 september, 2024 kl. 14:17 #9469
Jag tror det blir ytterligare ett par efterskalv men omöjligt att vara säker förstås.
Vet att du obsade UZ Boo kvällen den 30 aug men legitimerade SVO-kontrollanten låter meddela att de inte kommit in ännu.
-
1 september, 2024 kl. 14:53 #9470
Oj, miss. Jag rapporterar in grejer på 3 olika ställen (SVO, AAVSO, BAA-VSS eller CBA) och det blir lite rörigt ibland…
Nu ska de vara där.
Ovanpå allt man glömmer så kollar inte AAVSO om man redan HAR rapporterar in samma – flera gånger har jag rapporterat dubbelt och sen fått sitta och deleta… manuellt… en i taget…
SVO är förstås mycket bättre på detta!
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
1 september, 2024 kl. 15:26 #9471
-
1 september, 2024 kl. 21:22 #9473
Hej!
Efterskalv uppenbart pågående. Ca 14 med C-filter.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294-
Det här svaret redigerades för 1 år av
 Magnus Larsson.
Magnus Larsson.
-
Det här svaret redigerades för 1 år av
-
2 september, 2024 kl. 17:47 #9479
Hej!
En fallande trend igårkväll, uppenbarligen ett kort efterskalv:
Har vi nån idé om vad det är vi ser här? Det är ju variationer på flera magnituder på kort tid. Att det är ackreationsskivan som lyser upp är väl klart, men varför svänger den så här?
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
2 september, 2024 kl. 20:05 #9480
Svåra frågor … jag har inget bra svar.
Dessa efterskalv hos UZ Boo är fascinerande. Om det skulle komma ett fjärde, och sedan inga fler, så har mönstret från både 2003 och 2013 repeterats på ett nästan överraskande sätt.
En tanke vore att jämföra efterskalven med AAVSO-data från motsvarande händelser 2003 och 2013. Speciellt efterskalven 2013 blev mycket väl dokumenterade, bland annat finns en serie under ett mycket snabbt stig. Finns någon periodicitet som återkommer nu 2024?
De aktuella perioderna var ungefär 20 dec 2003 till 3 jan 2004 och 9 aug 2013 till 26 aug 2013.
Att på något sätt ”samköra” de (hittills) 11 kända efterskalven är en intressant tanke.
PS:
Magnus, jag vill inte stressa dig men AAVSO har inga obsar från 30 augusti (de finns i SVO).
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
-
3 september, 2024 kl. 07:52 #9503
Hej!
Absolut ingen stress – uppenbarligen fallerade min normala process den 31/8 och det är hjälpsamt att du kollar! 🙂
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
3 september, 2024 kl. 09:57 #9504
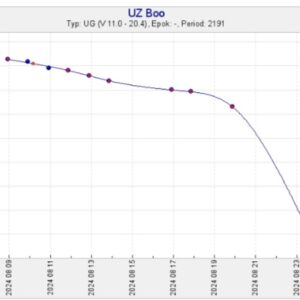
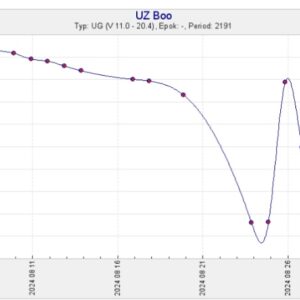
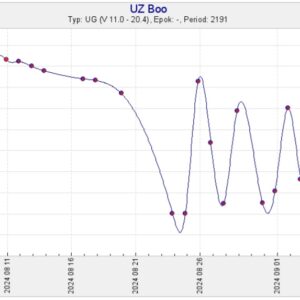
Då kör vi en ny och uppdaterad SVO-kurva för UZ Boo!
Obs-serien är nästan surrealistiskt bra, med mätningar nästan alla kvällar sedan huvudutbrottet skedde. Man skulle kunna tro att diagrammet visar den samlade insatsen från variabilister i världen! Utbrottet kom tidsmässigt rätt lägligt, även om stjärnan ligger ganska lågt på himlen, eftersom augusti hos oss är årets stjärnsäkraste månad. Tillräckligt mörkt men ändå nära sommarens många klara men ljusa nätter.
PS:
En sak som förvirrar mig en smula, när jag kollar de tre efterskalven i år, är att perioden redan vid en snabb blick tycks ligga kring 3 dygn … men magnitudtendenserna under de enskilda obs-serierna passar inte in. Kan det dessutom finnas en typ av snabbare (superpuckelaktiga?) variationer som gör sig gällande?
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
4 september, 2024 kl. 09:48 #9519
Igår kväll (3 september) var UZ Boo ljussvag, V-magnitud 16.5 enligt mätningar av Ian Sharp. Kanske har stjärnan nu tröttnat på efterskalv, det blir kanske inget fjärde? Har slutavtagandet inletts? Vi får se.
-
5 september, 2024 kl. 19:41 #9527
Hej!
I snitt ca 16,2 med C-filter här igårkväll.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
5 september, 2024 kl. 21:28 #9528
Spännande!
Om det inte blir något efterskalv ikväll (5 sep) så är kanske stjärnan på väg neråt mot djupare magnituder? Kan bli det ena eller andra.
Är du på väg till Öland?
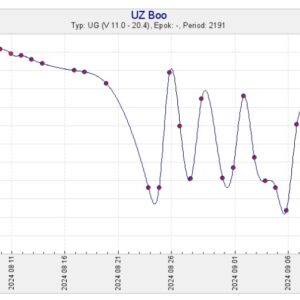
Uppdaterad SVO-kurva, se nedan.
Attachments:
-
6 september, 2024 kl. 06:51 #9530
Hej!
Inget efterskalv igår (5/9). Jag har den på ca 17 med C-filter, vid en snabb koll av nattens fångst.
Inget Öland för mig i år – är inne i intensiv terminsstart på Lunds universitet som inte ger så mycket utrymme för utsvävningar …
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
6 september, 2024 kl. 14:05 #9531
Mycket möjligt att det inte blir några fler efterskalv.
En påfallande sak är att utbrotten 2003, 2013 och nu 2024 liknar varandra så mycket. Samma djupa dip (som för tankarna till DQ Her-novor) och samma efterskalv. Således en rätt komplex utveckling som återkommer. Ackretionsskivan är förstås djupt insyltad i detta även om jag inte riktigt vet hur.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
7 september, 2024 kl. 16:13 #9547
Hej!!!
Nu kom det, ett efterskalv till:
C-filter igårkväll.
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
8 september, 2024 kl. 10:16 #9606
Hej!
Jag lyckades inte mäta ordentligt igår – fick en bild med ett mätfel på 2.4 magnituder… men den var uppenbarligen fortfarande ljus! Så kanske en lite längre topp denna gången. David, har du lyckats fånga den?
Magnus
C11, C8, Skywatcher ED100 Pro
Celestron CGE-Pro, Losmandy G11, Celestron AVX
QHY268m, QHY183, ASI183, ASI294 -
8 september, 2024 kl. 10:21 #9609
Tyvärr inte. Har varit på öland och behövde sova ut igår efter några nätter ute under stjärnorna.
/David
SVO: DHE
AAVSO: HDAE -
9 september, 2024 kl. 09:44 #9620
Hej,
Fick nätt och jämnt en bild på UZ Boo igår kväll den 8:e september med MWT från Oria och mätte den till V-magnitud 16,9.
/David
SVO: DHE
AAVSO: HDAE -
9 september, 2024 kl. 10:33 #9621
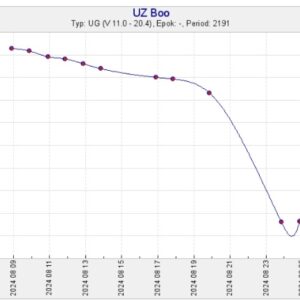
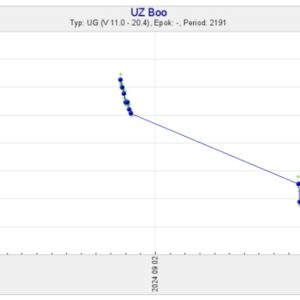
Efter mätningen med MWT den 8 september sitter det som en smäck att uppdatera SVO-kurvan, se nedan.
Minima mellan efterskalven liknar egentligen väldigt mycket själva dippen direkt efter huvudmaximet, så rent fysikaliskt har de kanske samma orsak?
Attachments:
-
9 september, 2024 kl. 22:34 #9647
V-magnitud nu ikväll den 9 september är 17,4. Fotometri från MWT i Oria.
/David
SVO: DHE
AAVSO: HDAE -
10 september, 2024 kl. 11:12 #9648
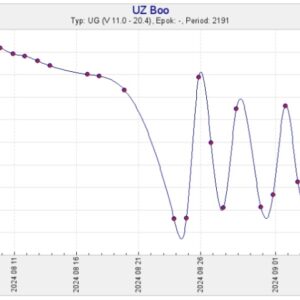
Då kör vi för omväxlings skull ett AAVSO-diagram den här gången. Det blir nästan identiskt med ett SVO-diagram eftersom det är SAAF som står för en majoritet av materialet.
Om det nu blir så att efterskalven är över, så kan man spontant tycka det är lite kuriöst att det blivit alldeles exakt fyra efterskalv 2003, 2013 och 2024. Kanske mest en slump att antalet efterskalv kopierats? Eller inte. Svårt att veta. Och det kan förstås inte uteslutas att det kommer ett femte denna gång.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
12 september, 2024 kl. 15:53 #9665
Inga indikationer på ytterligare efterskalv i AAVSO-datan från bl.a. Sharp. Har vi nu sett det sista från UZ Boo på några år?
/David
SVO: DHE
AAVSO: HDAE -
12 september, 2024 kl. 19:57 #9669
Ja, nu tror jag att det är slut på det som hos klassiska novor brukar kallas transitionsfasen. Magnituden är ju nu nere på nästan 18, och det återstår nog bara ett slutligt avtagande till 20.
Det ligger väldigt nära till hands att göra ett diagram där utbrotten 2003, 2013 och 2024 jämförs, med AAVSO-data (V och CV). Kanske alla tre utbrotten i samma diagram, där man sätter utbrottstiden till noll och förskjuter magnitudskalan på lämpligt vis mellan de tre utbrotten så att kurvorna separeras.
Någon som anmäler sig frivilligt? Excel är lämpligt verktyg, finns säkert andra program också. För egen del använder jag nästan aldrig dator (har ingen som är aktiv) efter pensioneringen (musarm) så jag avstår gärna. Men jag tycker absolut det bör göras… det borde vara något för Telescopium.
-
Det här svaret redigerades för 1 år av
Hans Bengtsson.
Attachments:
-
Det här svaret redigerades för 1 år av
-
-
FörfattareInlägg
- Du måste vara inloggad för att svara på detta ämne.
Senaste diskussionerna
-
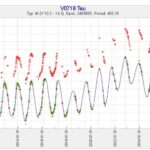
V0718 Tau
svar av
 Magnus Larsson
Magnus Larsson
-
Aktuell solaktivitet
svar av
Hans Bengtsson
-
Projekt m31 Andromeda
svar av
 Gabriel Wiklund
Gabriel Wiklund
-
ER UMa
tråd av
 Magnus Larsson
Magnus Larsson
-
NGC 2841 – Tigerögat
tråd av
 Gabriel Wiklund
Gabriel Wiklund
-
Fiskmåsnebulosan
tråd av
 Johan Warell
Johan Warell
-
Sektionsmöte den 12/3
tråd av
 Magnus Larsson
Magnus Larsson
-
En timme på Messier 33
svar av
 Johan Warell
Johan Warell
-
Fossilspårsnebulosan NGC 1491
tråd av
Hans H
-
NGC 3147
tråd av
 Gabriel Wiklund
Gabriel Wiklund
-
Messier 33
tråd av
robin
-
MU Cam
svar av
 Magnus Larsson
Magnus Larsson
-
Konstigt fenomen
svar av
Dennis Akbari
-
240 P/NEAT och fragment 240P-B
tråd av
Hans H
Månadens bild i galleriet
Årets bild i galleriet
 Senaste nytt från SAAF-webben
Senaste nytt från SAAF-webben
- Årsmöte 2026
- Vårhimlens pärlor – observationskafé med SAAF
- Leoträffen – ny observationsträff på Öland!
- Årets första variabelmöte 12 mars – välkommen alla SAAF-medlemmar
- Värmland Star Party 2026
- Apertur blir SAAF:s nya medlemstidskrift!
- Telescopium nummer 4 2025 snart ute – 93:e och sista numret!
- Observationsbeställningar – nytt sätt att ta bilder med fjärrteleskopet
- Telescopium nr 3 2025 ute snart!
- Årsmöte 2025
Kalendariet


Antal unika dagsbesökare (unika IP)
Idag: 39 st
Senaste 7 dagarna: 280 st
Senaste 30 dagarna: 6200 st